LipSyncをDIYする（後編）

こんにちは。

株式会社Synamonでエンジニアをしております、渡辺(@mochi_neko_7)と申します。

本記事は

synamon.hatenablog.com

の後編になります。

まずは確認も含めて簡単に前編のおさらいをしましょう。

前編のおさらい

リップシンクをするにあたって、音声データを解析してその母音を推定して口を動かそうというのが今回紹介する手法の大きな流れになります。

母音を解析するための手法はフォルマント解析と呼ばれ、今回は次のような流れで音声データの処理を行います。

音声データの取得
必要なデータの抽出
正規化
高域強調（pre-emphasis）
ハミング窓にかける
自己相関関数からLPC係数と残差分散を計算
LPC係数と残差分散をデジタルフィルタにかけてスペクトル包絡線を計算
ピークの抽出
母音の推定

前編では１から６までの処理で、実際の音声データから、いくつかの前処理ののち、LPC係数 $a [ i ]$ と残差分散 $E [ i ]$ が得られました。

後編はフォルマント解析の手順の７からになります。

７.　デジタルフィルタ

LPCによって得られたLPC係数と残差分散から、実際のスペクトルの包絡線を求めなくてはなりません。

そこで用いるのが、デジタルフィルタと呼ばれるものです。

正直、著者はこのデジタルフィルタとは縁がなかったので、結果やるべきことを述べるだけになってしまうことをご容赦ください。

まずは、Z変換と呼ばれる変換があります。

　 $\displaystyle X [ z ] = \sum_{n = 1}^{N} z^{-n} x [ n ]$

ここで、 $X$ が出力、 $z$ が変換を特徴づける複素数、 $x [ n ]$ が入力、 $T$ が入力データの長さになります。

この $z$ として $z = e^{i \omega}$ を用いる際には、よく知られた離散フーリエ変換（DFT）の変換の式

　 $\displaystyle X [ \omega ] = \sum_{t = 1}^{T} e^{- i \omega t} x [ t ]$

に帰着します。

デジタルフィルタにはいくつも種類があるようなのですが、Z変換を用いたデジタルフィルタとして、次のようなものが知られています。

　 $\displaystyle H [ z ] = \frac{A [ z ]}{B [ z ]}$

　 $\displaystyle A [ z ] = \sum_{n = 0}^{N} z^{-n} a [ n ] \ , \ B [ z ] = \sum_{m = 0}^{M} z^{-m} b [ m ] \ , \ b [ 0 ] = 1$

ここで、 $a$ と $b$ が二種類の入力になります。

これを、 $a$ として残差分散 $E [ i ]$ 、 $b$ としてLPC係数 $a [ i ]$ 、 $z$ として $z = e^{i \omega}$ を用いて、各 $\omega$ に対して計算することによって、目的の周波数の応答が得られるようです。*1

＊ $a$ は係数なので無次元、 $E$ が振幅なので長さの次元、出力は周波数なので長さの逆次元となり、丁度次元的には合っているのは分かります。

（2018/9/17追記）

これってよく見たら分母分子それぞれただのフーリエ変換ですね。

するとFFTなどを用いた方が早いかもしれません。

フーリエ変換を紹介したところでも述べましたが、得られるスペクトルの出力は一般には複素数です。

ですので情報としては、絶対値(振幅) $|z|$ と位相 $\theta$ の二つがあります。

　 $\displaystyle z = |z| e^{ i \theta}$

今回の解析では位相の情報は必要ありませんので、フィルタにかけた出力の絶対値のみ取り出します。

したがって最終的には、残差分散 $E [ i ]$ とLPC係数 $a [ i ]$ を用いて、次を計算します。

　 $\displaystyle |H [ \omega ] | =　\left| \frac{ \sum_{t = 0}^{T - 1} e^{ - i \omega t} E [ t ] }{ \sum_{t = 0}^{T - 1} e^{ - i \omega t} a [ t ] } \right|$

＊複素数に馴染みのない方のために、絶対値 $| \ |$ の計算のためには、直接複素数を計算するよりは、有名なEulerの関係式

　 $\displaystyle e^{i \theta} = \cos \theta + i \sin \theta$

を用いて、

　 $\displaystyle |z| = \sqrt{ Re(z)^2 + Im(z)^2 }$

のように自分で計算しても構いません。

$Re(z)$ は実部、つまり $e^{i \theta}$ を $cos \theta$ に置き換えて和を取ったもので、 $Im(z)$ は虚部、つまり $e^{i \theta}$ を $sin \theta$ に置き換えて和をとったものになります。

これを各周波数で、分母分子でそれぞれ和を計算して比をとればよいです。

実際にこれまでの処理の後の音声のスペクトル包絡線を描いてみると、

　　　　　　　 f:id:mochinekos:20180909134326p:plain

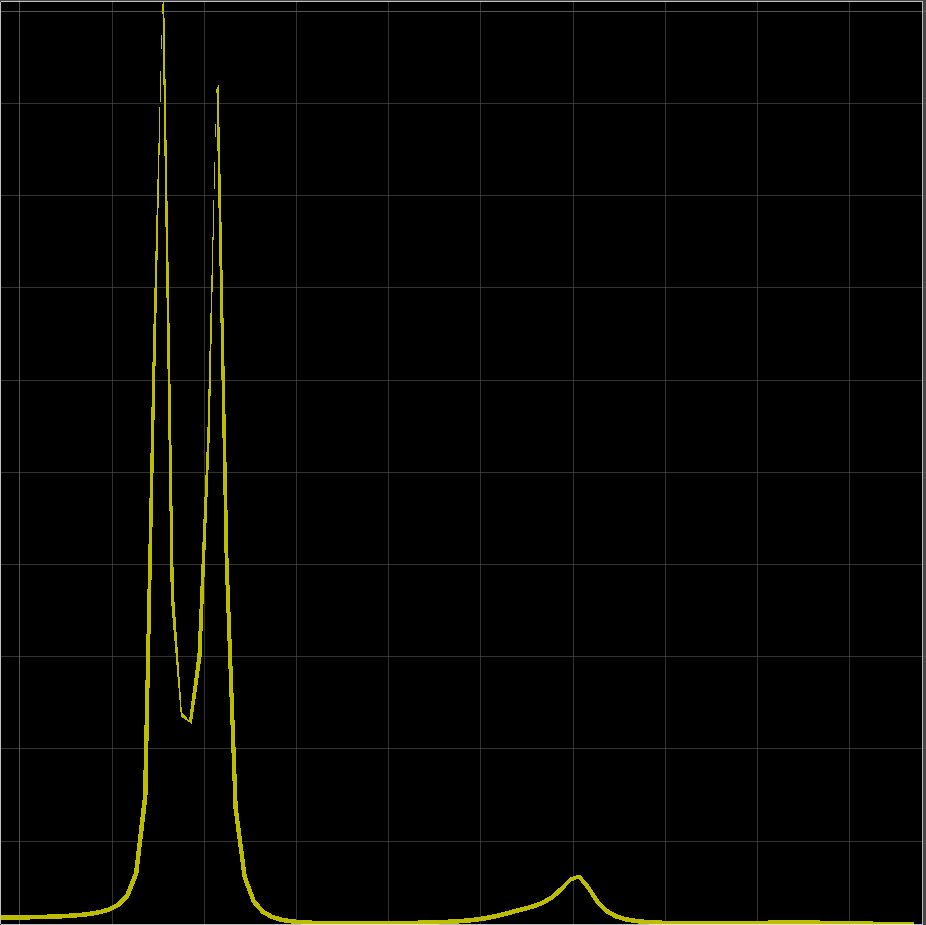
のようになだらかな曲線が得られます。（先ほど載せたLPC次数50のものと同じです）

始めのFFTによるスペクトルと比較してみると分かりやすのではないでしょうか？

このはじめの２つのピークが、目的の第１・第２フォルマント周波数になります。

８.　ピーク抽出

これで周波数の分布が得られましたが、フォルマント解析ではそのピークに着目します。

周波数の小さいものから順に、第一フォルマント周波数(f1)、第二フォルマント周波数(f2)、...のように呼ばれます。

母音を推定するには、第二フォルマントまで取ればいいようです。*2 *3

少し上でも触れましたが、得られる周波数分布は配列のインデックス毎で、その解像度は実際に用いるサンプル数によって決まりました。

すると単純にピークの値を取るだけでは、その精度は完全にその解像度で決まってしまいます。

ですが実際にはその解像度をそこまで良くするのは負荷的にも苦しい場合が多いので、ここで少し工夫をしましょう。*4

まずは、低解像度で得られるピーク位置に対して、それに隣り合う区間内に本当のピーク位置があると仮定します。

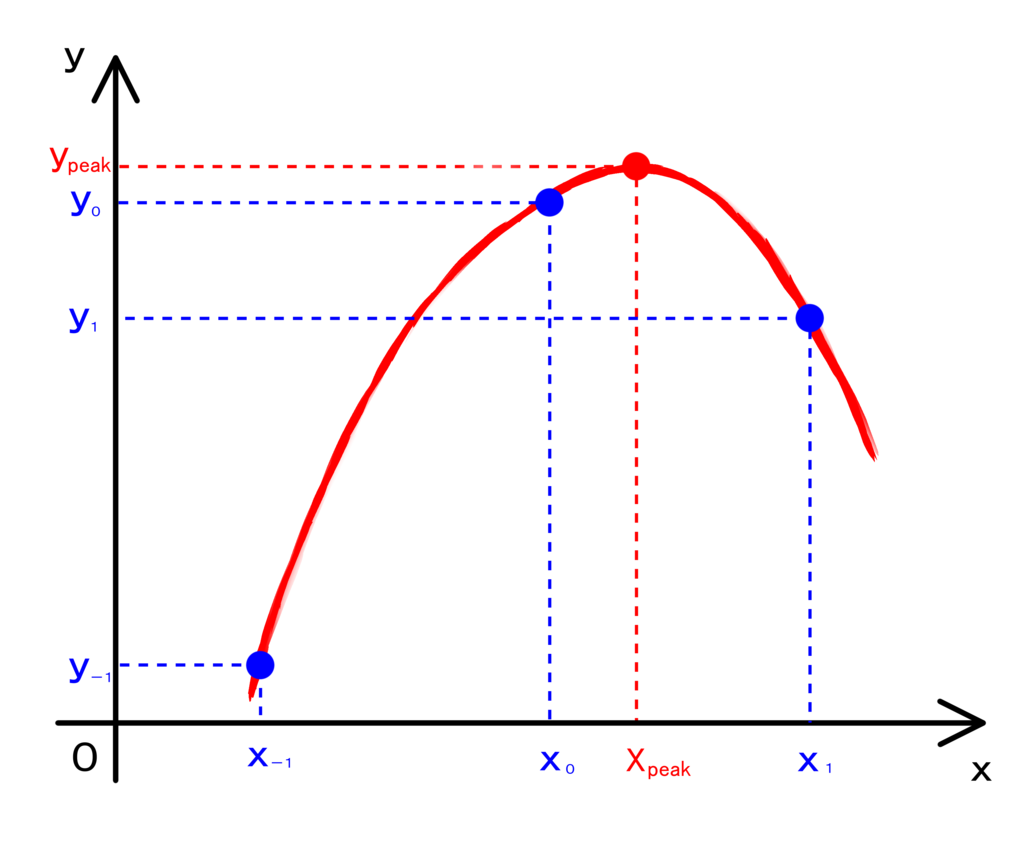
そして得られたピーク位置とその両端の位置を全て通る放物線を仮定し、その放物線のピークの位置で真のピーク位置を推定します。

放物線の式（二次関数）を思い出すと、例えば

　 $\displaystyle y = a x^2 + b x + c$

　 $\displaystyle \ \ = a (x - p)^2 + q \ , \ p = - \frac{b}{2a} \ , \ q = c - \frac{b^2}{4a}$

のように $x$ を横軸、 $y$ を縦軸の座標として書いた場合には、平方完成した $(p, q)$ が放物線のピークの座標に対応します。

未知の定数は $a, b, c$ の３つありますので、放物線を通る３点の座標が分かっていればこれらの定数が決まります。*5

実際の計算では、 $x$ 軸に対応する周波数の幅が固定なので少し簡略化できます。

元のピークの $x$ 座標を０に取り、その両端の $x$ 座標を－１、１とすると、

　 $y[-1] = a - b + c$

　 $y[0] = c$

　 $y[1] = a + b + c$

のような関係から $a, b, c$ および $p, q$ が容易に求まります。

　 $\displaystyle c = y[0]$

　 $\displaystyle a = \frac{y[1] + y[-1]}{2} - c$

　 $\displaystyle b = \frac{y[1] - y[-1]}{2}$

最後に得られた $p$ はこの設定の場合には周波数の幅に対する比に対応しますので、始めに得られたピーク $\omega_{peak}$ から、周波数解像度 $\delta \omega$ を用いて

　 $\hat{\omega}_{peak} = \omega_{peak} + p \delta \omega$

のように、ピーク位置の周波数を推定します。

f:id:mochinekos:20180913180234p:plain

このようにして、ピーク位置を推定しつつ、周波数の小さいところから二つ抽出してフォルマント周波数とします。

＊場合によっては周波数が0の辺りにピーク（第０フォルマント）ができてしまう場合がありますが、基本的にはそれは無視して構わないと思います。*6

９.　母音の推定

いよいよ２つのフォルマント周波数が得られましたので、これから母音を推定します。

まず人の母音の周波数には、次の図のような傾向があるとされています。

f:id:mochinekos:20180915134847p:plain

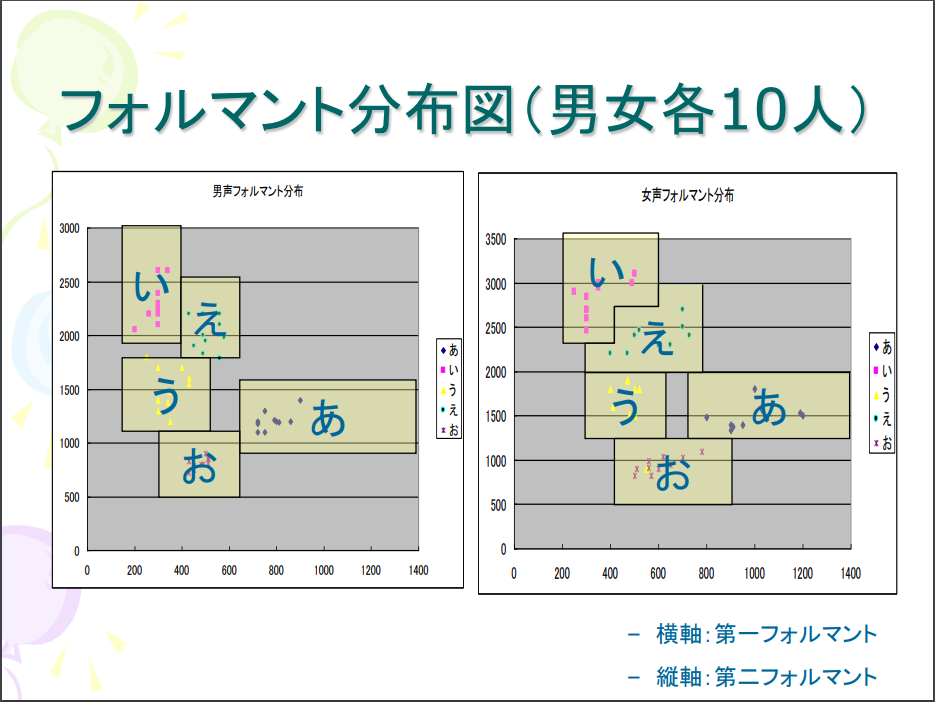
引用元：

http://www.sps.sie.dendai.ac.jp/blog/wp-content/uploads/2008/04/kiso_b.pdf

性別によって少し分布が平行にずれますが、基本的には同じような構造をもっていると知られています。

そのような構造を持つ理由は、人の発声のメカニズムにあるようです。

声はまず声帯で振動が発生しますが、喉、口腔、鼻、唇などでその音は共鳴します。

特に母音は口の形で特徴付けられますので、口の形による共鳴が特徴的なスペクトルとなり、フォルマント周波数として観測できるということです。

従って、得られらフォルマント周波数と分布を比較して、その音声がどの母音に属するのか判定すればよいです。

理想的には、大勢の声をサンプリングして普遍的な分布を抽出して用いるのがよいと思われます。

現実的には難しい場合もありますので、妥協策としては個人の特性に合わせて調整（キャリブレーション）するのも考えられます。

経験的には、個人なら傾向が分かりやすいのでそれほど難しくはないと思います。

一番愚直な判定方法としては、各母音の集合の重心を決め、その中から最も近い母音と推定する方法が考えられます。

より適切な分布の用い方、判定方法もあるのではと思いますが、今回は時間の都合でそこまであれこれ試したりはできませんでした。

フォルマント解析の手法に関する解説は以上になります。

負荷軽減

音声はデータ数が多く、特に周波数解析をするための変換は二次元的な計算量になることが多いので、負荷が高くなりがちです。

特にVRに使いたい場合には、フレームレートの低下はVR酔いの原因となりますので、処理が重すぎる場合には採用するのは難しくなります。

筆者が最初に書いた分かりやすさ重視のコードでは、サンプル数1024で、ムラはありますがだいたい毎フレーム13ms程度の負荷でした。*7

当然他のスクリプトやグラフィックの処理の負荷も実際にはありますし、これでは到底使いものになりません。

そこで、最適化で負荷が軽減できないか調べてみることにします。

具体的な検討をする前に、まずはどのような処理が負荷が大きいのか把握しておく必要があります。

例えば今回のケースでは、

音声データそのものが大きい配列である
配列全体に渡る処理が多い
特に周波数に変換する際には、おおよそ二次元的な反復処理が必要
単体の計算負荷が重いものもある（コサインや平方根など）

などが考えられます。

まずは一番素直に、サンプル数が多いのではと疑うことができます。

Unityのデフォルトの1フレームでの1チャンネルあたりのサンプル数が1024でした。

これを半分の512に減らしてみると、おおよそ2/3程度の負荷になりました。*8

ただし、上で説明しましたがサンプル数と周波数解像度はトレードオフの関係にあります。

サンプル数を減らす場合は、実際の母音の判定に影響の出ない範囲で行ってください。

大きな最適化としては、計算アルゴリズム自体の検討が考えられます。

例えばフォルマント周波数を求める方法はいくつかありますが、周波数に変換する処理はかなり負荷が大きいので、できるだけ少ない回数にするか、高速に計算できるアルゴリズムを用いるべきです。

既に知られている方法を用いるのであればいいのですが、新たなアルゴリズムを作るのはさすがに大変になります。

今回紹介したLPCを用いた方法は比較的処理の少ないアルゴリズムのはずです。*9

次に考えられるのは、処理の並列化です。

音声データはベクトルであり、周波数への変換はおおよそ行列的な計算になりますので、for文などによる反復処理の負荷が大部分を占めます。

そこで、反復処理をスレッド分割するということが考えられます。

簡単に実装するなら、例えばC#ならfor文をSystem.Threading.Tasks.Parallel.Forに置き換えるなどができます。

他にもUnityでの実装は、最近追加されたJobSystemを用いる方法や、Compote Shaderを使う方法も考えられます。

ただし注意しなければならないのは、全部を全部並列化すればいいという訳ではないということです。

並列化はその性質上、反復する処理がそれぞれ独立しているのが望ましいです。

同一の変数にアクセスする際などには注意する必要があります。

並列化の際の注意点は広く知られていると思いますので、詳細はその手の参考書などを読んでいただければと思います。

筆者がParallel.Forを用いて並列化したところでは、13msから4ms程度まで負荷を軽減することができました。

ここから更に最適化をしたい場合には、計算回数をできるだけ減らしたり、個々の処理をできるだけ軽くするなど、細かな調整をすることになります。

筆者はあまり詳しくはないのですが、コンパイラやアセンブリのレベルで負荷を減らすなどの工夫はできると思います。*10

要求されるパフォーマンス次第で工夫して頂ければと思います。

あるいは最適化の上で負荷が現実的ではない場合には、音声解析的なアプローチを断念しなければならないこともあるかもしれません。

だいぶクオリティは落ちますが、例えば音声の音量のみ観測してそれっぽく口の形を動かすだけというのも可能です。

そのあたりも優先順位次第では検討しなければならない場合も出てくると思います。

最新版のNEUTRANSではマルチプレイとネットワークの都合から、β版として簡易版のリップシンク実装と、併せてアバターの目の瞬きも実装しています。*11

課題

最後に、今後の課題をいくつか挙げます。

母音の推定のアルゴリズムの研究が不十分
まだ最適化が十分でない（依然負荷は高い）
マルチプレイ・ネットワークの対応が不十分

音声の解析そのものはそこそこ安定はしたのですが、母音の判定方法の工夫をする時間が取れませんでした。

フォルマント分布図の用意の仕方、判定方法、機械学習的なアプローチなど、まだまだやれることはありそうです。

最適化も当初に比べたら大きく軽減はできましたが、他の処理と比較すると圧倒的に負荷は高いです。

UnityのJobSystemもまだ試していませんし、逆アセンブリなどの詳細な解析もまだなので、最適化の余地はあると思います。

マルチプレイ環境下で遅延なしに解析を行うなら、他人の音声の解析までしている余裕はありません。

実際の音声の発音に遅延しないようにするには、音声の送受信のタイミングや順序に気を付ける必要があります。

最終的にはこれらの課題を解決しつつ、本格的なリップシンクをネットワーク・マルチプレイ環境下で提供できればと思っています。

最後に

かなり長くなってしまいましたが、いかがだったでしょうか。

単に必要な処理を述べるのではなく、その意味を理解することに重点を置いて解説したつもりです。

実際の実装をするにあたって知っておくべきこと、注意すべきことをできるだけ詳細に述べたつもりですが、至らない点もあるかもしれません。

よくわからない部分や、間違っている個所など、気になるところがありましたらお気軽にご連絡していただければと思います。

最後まで読んで頂きありがとうございました。

＊おまけ

Unityでマイクの音声を取得する際、UnityEngine.Microphoneクラスを利用するのがお手軽ですが、いくつか注意点があります。

ネットで指摘しているものを見かけなかったので、参考になれば幸いです。

AudioClipはstaticメソッドのMicrophone.Start(...)によって取得できるのですが、既に他所でこれを利用している場合には、古いほうのAudioClipの内容が更新されなくなってしまいます。

結果として古い音声がループ再生されるなどの現象を引き起こす場合があります。

例えばPhotonVoiceを利用しているのであれば、注意が要ります。

回避策としては、マイク音源を複数が利用できるよう代理でキャッシュするクラスを作成し、Microphoneクラスを直接用いないようにすればよいです。

ただしその場合にはPhotonVoice側の実装に手を入れる必要があり、バージョンの更新の度に修正しなければならない恐れがありますので注意してください。

かといってマイクを利用するクラスたちが、わざわざPhotonVoiceなどの特定のものに音声を聞きにいくのもかなり不自然ですので悩ましいです。

（2018/9/17）誤字修正

参考

[1] 「音声情報処理」古川貞煕（森北出版株式会社）

[2] 「実験音声学のための音声分析」平坂文男（関東学院大学出版会）　

http://www.sps.sie.dendai.ac.jp/blog/wp-content/uploads/2008/04/kiso_b.pdf

*1:zの選び方はともかく、なぜこれでよいのか正直よく理解はできていません。そもそもデジタルフィルタ自体に馴染みがないからでしょうか？

*2:詳しくは知りませんが、子音を推定するときにはf3、f4まで見るようです

*3:あるいは多くとれば母音の推定の精度が上がると言っている人もいます（そこまで検証できていませんが）

*4:何も考えず得られるピークを用いてもそこまで悪くはないのですが

*5:三元の連立方程式ですね

*6:それを防ぐ手法もあるようです

*7:これだけで明らかに90fps = 11.1msを超えていますね...

*8:最適化後、UnityEditor上で測りました

*9:例えばケプストラムを用いる方法では、何度かフーリエ変換をする必要があります。

*10:その場合にはコードの可読性が犠牲になることも

*11:自分の声のみのリップシンクに限るなら問題はないレベルです

前編のおさらい

７. デジタルフィルタ

８. ピーク抽出

９. 母音の推定

負荷軽減

課題

最後に

＊おまけ

参考

７.　デジタルフィルタ

８.　ピーク抽出

９.　母音の推定