こんにちは。
株式会社Synamonでエンジニアをしております、渡辺(@mochi_neko_7)と申します。
VRでは自分の好きなアバターになれるというのは大きな魅力の一つではないかと思いますが、せっかくのアバターも固い表情のままではちょっともったいないですよね。
そこで今回はアバターに表情を付ける一つの方法として、プレイヤーの話している声からアバターの口を動かすリップシンクとよばれる手法についてご紹介したいと思います。
今日では、リップシンクを手軽に利用できる環境もいくつかありますが、その中でこのお話をさせていただくのは、ブラックボックスをあまり使いたくないという想いと、パフォーマンスなどの要求から自分で実装したい場合があるのではないかと思ったからです。
ネットにも技術的な部分を詳しく解説している記事があまり見つからず、筆者自身未知の領域で苦労した経験から、初心者の方にも分かりやすく説明できればと思います。
本記事は、リップシンクを自分で実装したい、でも音声の専門知識があるわけではない、数学なら少しは分かるから何をやっているのか理解しながら実装したい、という趣旨でお話をします。
前提となる知識ですが、簡単な音の知識*1に加えて、ちゃんと理解するのであれば線形代数、フーリエ変換の知識があるのが望ましいです。
弊社の『NEUTRANS』はUnityで開発しておりますのでUnityの話にも少し触れますが、基本的な部分は開発環境・言語には依りません。
なお今回の記事を書くにあたって、凹みさんの以下の記事も参考にさせていただきました。
紹介する全てではありませんが、一部こちらにはC++のサンプルコードも掲載されていらっしゃいますので、併せて参考にしていただければと思います。
また、筆者は音声解析は門外漢ですので、間違ったことも多分に含まれるかもしれません。
筆者の知識の範囲内で理解している部分しか説明できませんので、あまり詳しく触れていない部分もあります。
もし間違いや不適切な部分にお気づきの方がいらっしゃいましたら、ご指摘いただけると幸いです。
本記事は前編・後編の二章立てになります。
少し前置きが長くなりましたが、それでは本題に入りたいと思います。
リップシンクとは
リップシンクとは、人の話す口の形とアバターの口の形を同期(Synchronize)させようというものです。
いわゆる”口パク”ですね。
たとえばアニメや最近のバーチャルYoutuberなんかでも、セリフを喋っている時は口が動きますよね。
口が動いているのといないのでは、そのキャラの存在感が大きく変わります。
セリフが決まっているならそれに合わせて動かせばいいだけですが、リアルタイムの音声に動きを合わせようとすると、どうしても音声データを解析する必要が出てきます。
特にリアルタイム性の強い生配信やVRでは、これをリアルタイムに行わなくてはなしません。
そこで、どのようにその音声データを解析して、話している口の形を調べるのか、という話になります。
今回紹介するのは、そのようなアプローチの一つになります。
解析手法
最もシンプルなリップシンクは、口の形を決める大きな要因である母音を知りたいというところから始まります。
そこで用いられるのがフォルマント(母音)解析と呼ばれるものです。
フォルマント解析にもいくつか手法がありますが、ここでは線形予測器(LPC)を用いる方法を採用します。
LPC係数からスペクトル包絡線を求め、そのピーク位置から第一フォルマント周波数(f1)と第二フォルマント周波数(f2)を決定し母音を推定します。
スペクトル包絡線を用いるのは、要するにスペクトル分布をなだらかにしてその特徴を捉えようということです。
このf1、f2の分布には、性別差はあれど大まかに母音毎の構造があるとされているので、これから母音を推定しようということです。
今回紹介する具体的な手順は次のようになります。
- 音声データの取得
- 必要なデータの抽出
- 正規化
- 高域強調(pre-emphasis)
- ハミング窓にかける
- 自己相関関数からLPC係数と残差分散を計算
- LPC係数と残差分散をデジタルフィルタにかけてスペクトル包絡線を計算
- ピークの抽出
- 母音の推定
大雑把に言えば、
・データの取得(1, 2)
・前処理(3, 4, 5)
・スペクトル分析(6, 7, 8)
・推定(9)
という流れです。
1.音声データの取得
まずは音声データがどのようなものか少し確認したいと思います。
Unityでは、AudioClipと呼ばれる形式で音声データは扱われます。
保存したデータも、マイクからの入力でも一緒です。
データ本体はAudioClip.GetDataで取得ができますが、中身は-1fから1fの範囲のfloat型の配列になります。
floatの各値は音の振動の変位を表しており、その絶対値が振幅になります。
配列のインデックス(整数)がチャンネル*2毎の時間*3に対応しています。
インデックス毎の時間間隔はサンプリング周波数*4によって決まります。
Unityでなくても、基本的には生の音声データは同じような形式と思われます。
デジタル化が少し適当ですが、ざっくり図にしてみるとこのような感じでしょうか。

音声の解析をする際には、変位の信号としてだけではなく、これをフーリエ変換して周波数の分布を調べるスペクトル分析がよく行われます。
離散化されたデータに対するフーリエ変換の高速なアルゴリズムとしては、FFTが有名ですね。
時間に対するフーリエ変換なので、得られるのはインデックスが周波数を表す配列になります。*5
一般にはこの出力の値は複素数ですが、絶対値をとることで各周波数の強度が得られます。
今回紹介する手法では、デジタルフィルタと呼ばれる別の手法がこの周波数解析に対応しています。
実際に解析をする際に音声データを取得する方法はいくつかありますが、例えばUnityでは、
- AudioClip.GetDataで直接
- AudioSource.GetOutputData
- OnAudioFilterReadイベントで受けとる
- マイクの音源をOSの機能で取得
などでしょうか。
リアルタイムの音声はもちろん、予め記録しておいた音源でも解析自体は変わりません。
2.必要な音声データの抽出
チャンネルは1つあれば十分ですので、複数チャンネルある音声データの場合には、まず1チャンネル分に限定しましょう。
また、データのサンプルの数もあまり多いとその分解析の負荷が大きくなってしまうので、適宜必要な数に絞ります。
ここで注意しなければならないのは、この抽出するサンプル数が周波数の解像度に関係している、ということです。
例えば、元の音声データのサンプリング周波数が44.1kHzの時に、サンプル数を1024と選ぶとします。
それから得られる周波数分布の配列の数はサンプル数と同じ1024で、その周波数領域はサンプリング周波数から0~44.1kHzになります。
したがって周波数解像度は、
になります。
この解像度がフォルマント解析に十分なのか注意する必要があります。
実際には各母音の構造のオーダーは小さいところで100-200Hz程度のようなので、この例だと許容範囲かなと思われます。
*今回の手法ではピーク抽出で少し補完をするので、実際にはこれより少し解像度が上がります。
3.正規化
音声の入力の大きさはものによってまちまちですが、音声の解析では基本的にはその大きさのスケールはあまり影響しません。
実際今回知りたいのは周波数の分布であって、大きさそのものではありません。
極端に値が小さいと計算精度的にもあまりよろしくありません。
そこで始めに-1~1の範囲に値が収まるようにリスケールします。
具体的には、絶対値の一番大きい値ですべての信号を割ればいいだけです。
弊社の社員の「あ」の声をサンプリングしてみると、

のようになります。
特徴的な周期性が見られますね。
これをFFTしてスペクトルをUnityのLineRendererで描いて見てみると、

少し線が見づらいですが、低周波部分に大きなピークがあるのが分かると思います。
ちなみに今回お見せするスペクトルのグラフは全て、全体44.1kHzの1/10の部分を切り取ったものになりますので、横軸は最大4410Hz程度です。
4. 高域強調(pre-emphasis)
音声解析では、実際の解析を始める前にいくつか前処理を行います。
この高域強調はその一つです。
その意味は高域(=高周波数領域)の成分を強調しようというものです。
フォルマント解析では少し高域のピークも見る必要があるので、これらの大きさを相対的に大きくできると解析しやすくで嬉しいです。
実際には次のように処理します。
ここで、が信号の配列(変位)、
がインデックス(時間)、
が定数係数で、これには1に近い0.95などの値が用いられるようです。
直前の時刻の変位の値に近いものを差し引くので、時間に対して変化が緩やかな信号は小さくなります。
つまり、周期の大きい(=周波数の小さい)成分が小さくなるので、結果として高域が強調されることになります。
先ほどの「あ」の音声を実際に高域強調してみると、
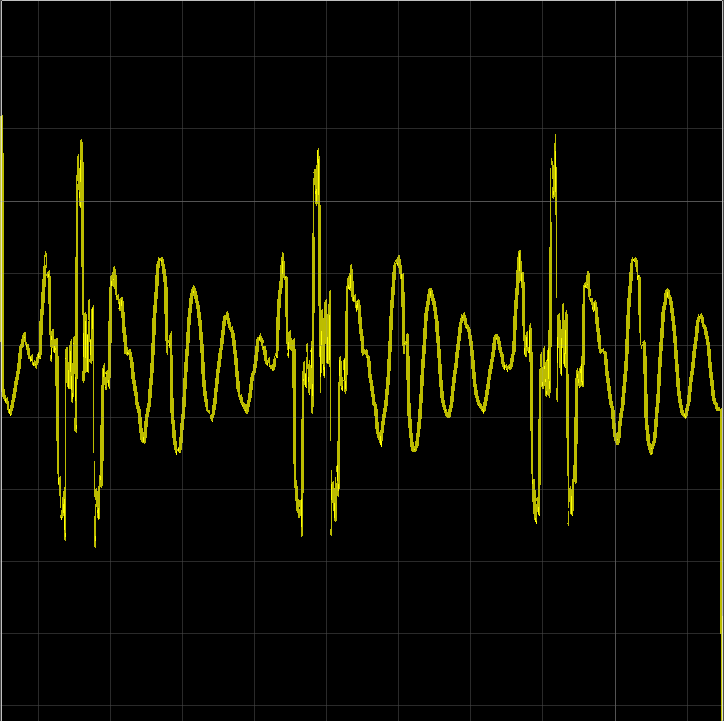
のようになります。
直接音声の波形を見てもどうなったか分かりにくいので、これをFFTしてみると、
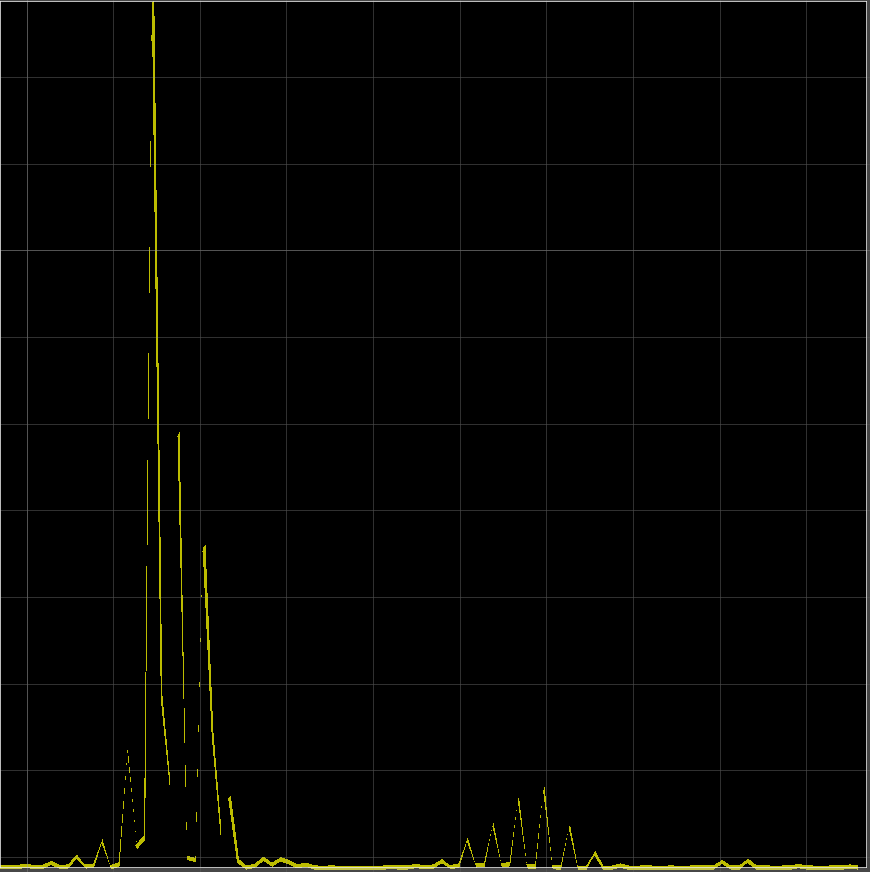
のようになりました。
ピーク以外の周波数、特にピーク直後の部分と、少し離れた高周波数の部分の成分が強調されて分かりやすくなったのがお分かりかと思います。
5. ハミング窓
周波数応答を得るにあたっては、基本的にはフーリエ変換(あるいはそれに相当する変換)を行う必要があります。
特に有限区間のフーリエ変換では、区間外での周期性が仮定されています。
そのため、信号の周期性(具体的には両端のデータの繋がり)が悪いと、得られるデータの性質が悪くなってしまいます。
そこで行われるのが時間窓をかける処理です。
今回はその中でも有名なハミング窓関数
を用いることにします。
ここで、がインデックス、
がサンプル数になります。
この窓関数をかけるので、実際には
のような計算を行います。
また今回も、先ほどの高域強調後の音声に対して、実際にハミング窓をかけてみてみましょう。
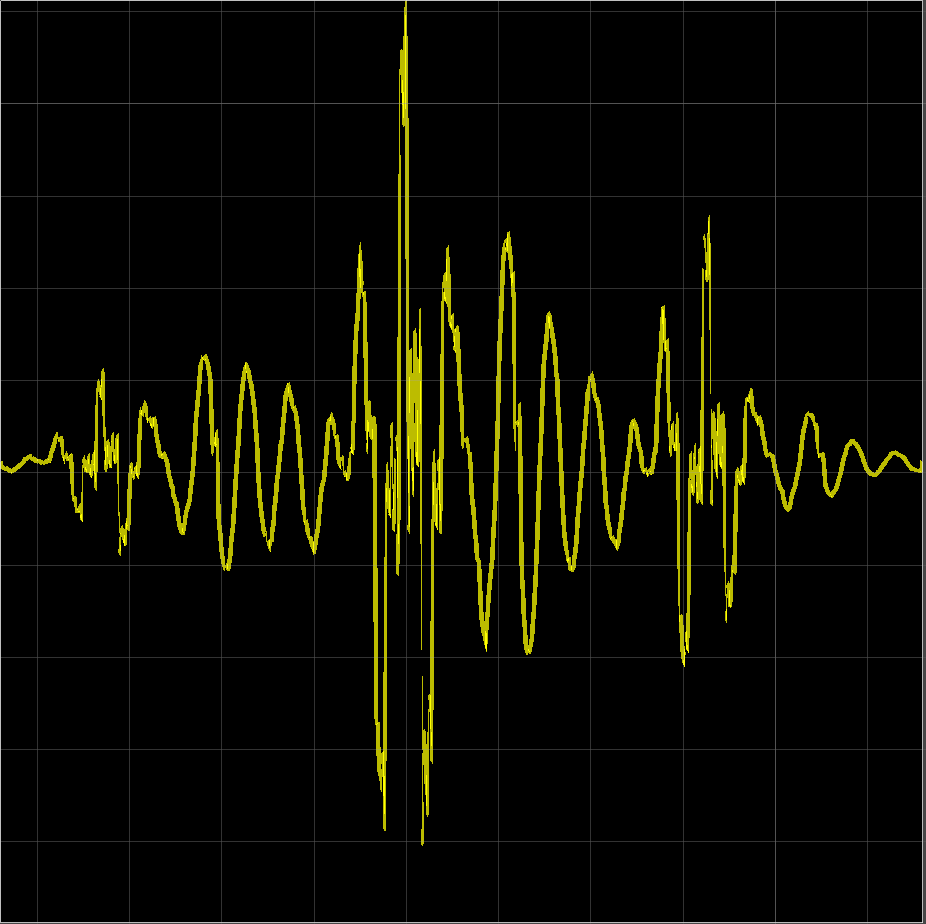
このように両端がすぼんで、両端での繋がりが良くなりました。
6. LPC
今回の手法のメインはこのLPC(Linear Predictive Coding:線形予測器)を用いる部分です。
詳しい解説はこちら
にもありますし、全部説明すると数式ばかりで長くなるので、細かな理論はこちらを参照して頂きつつ、ここでは概要と注意点を述べるにとどめます。
まずLPCとは、過去の信号から未来の信号を推定する方法の一つです。
具体的には次のような式を用います。
ここで、が時刻
の信号の推定値、
が過去の時刻(
)での信号、
がLPC係数、
がLPC次数になります。
この推定値と実際の値
との誤差が最小になるように、LPC係数
を選ぶのがこのLPCの課題になります。
線形という名前なのは、過去の信号の線形和、つまり定数係数の一次の和になっているからですね。
これを具体的に計算してみると、最終的にはYule-Walker方程式と呼ばれる形の行列方程式を解くことに帰着します。
幸いなことに、この方程式を効率的に解くLevinson-Durbin再帰法と呼ばれるアルゴリズムが知られていますので、これを用いましょう。
このような良いアルゴリズムが計算負荷を減らしてくれるのが、LPCを用いる上で嬉しい点です。
詳しい計算方法は、先ほどのリンク先を参照していただければと思います。*6
ただし、このアルゴリズムは逐次的なものですので、計算を並列化するのにはあまり向いていません。*7
この手法によって実際の信号をLPCの推定にかけ、少しなだらかなスペクトルの包絡線を得ようということになります。
ここで、まだ触れていないLPC次数に関して少し説明しましょう。
先ほどのLPCの推定の式の和を見ていただけるとお分かりかと思いますが、LPC次数はどの程度過去までの信号を考慮するのか、といったものになります。
これが小さすぎると、情報が少ないので大雑把な結果しか得られなくなり、逆に大きすぎると推定が強くなり実際のデータとの差が小さくなります*8。
今回欲しいのはあくまで大まかな傾向なので、このLPC次数をいい感じの値に設定する必要があります。
参考文献[2]では、このLPC次数の目安はサンプリング周波数(kHz)+4、5程度と言われています。
例えばサンプリング周波数が44.1kHzなら、程度でしょうか。
目安なので、実際のピークの出方を見ながら微調整するのがよさそうですが、実験的には確かにこの程度の値がちょうどいい感じになりました。
LPC次数を変えた結果を実際に比較して見てみましょう。
LPC次数の目安に近い50では、最終的なスペクトル包絡線は、例えば
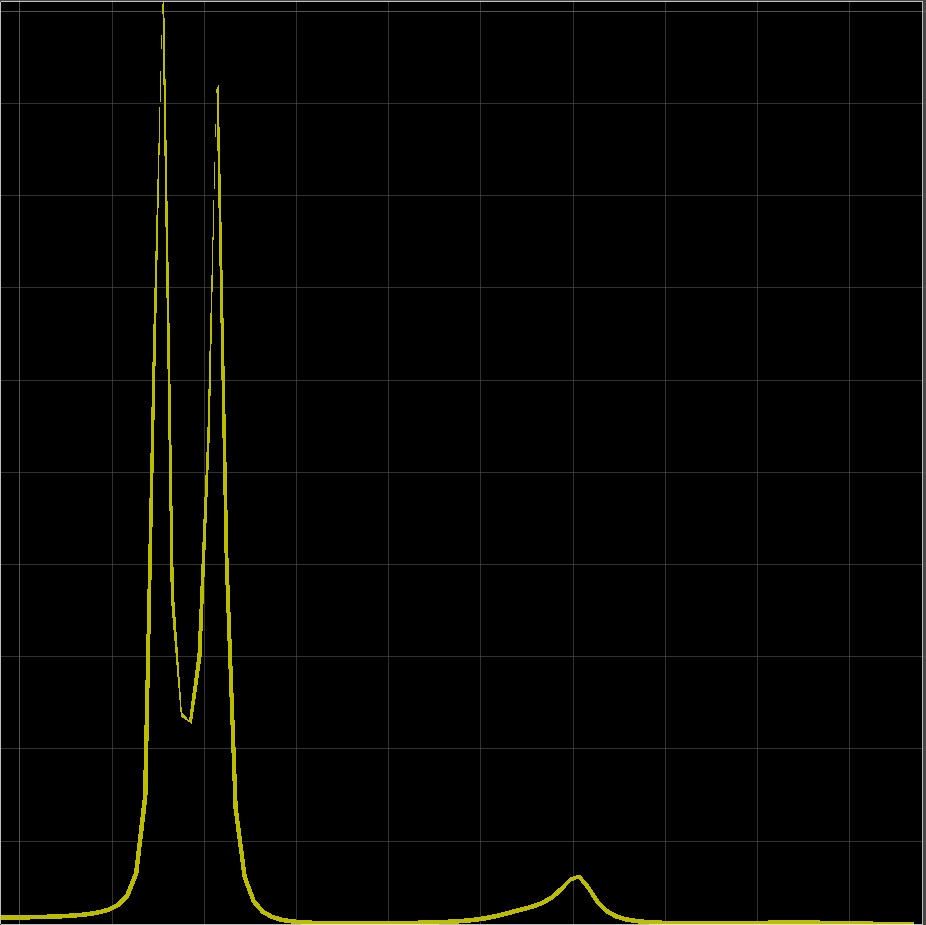
のようになります。
ここで次数を小さくして30にしてみると、

のように低周波での2つ目のピークが見えなくなってしまいます。
逆に次数を大きくして100にしてみると、

のように余分なピークが表れてしまいます。
どのようなピークが欲しいのかによってLPC次数の決め方は変わってしまいます。
これを全ての母音で、安定して欲しいフォルマント周波数が見えるよう次数を調整しなければなりません。
何かしら基準がないとかなり迷ってしまうところですので、上で紹介した目安を参考にしていただけるといいかなと思います。
こうして最終的には、LPC係数と残差分散
が得られます。
少し話が長くなってしまいましたので、中途半端ではありますが続きは後半でお話させていただきたいと思います。
後編はこちらです。
参考
[1] 「音声情報処理」古川貞煕(森北出版株式会社)
[2] 「実験音声学のための音声分析」平坂文男(関東学院大学出版会)